Project 3: Face Morphing

Part 1: Defining Correspondences

To morph two images, we need to select points of correspondences. I used the given tool to select points on the images. After defining the correspondences, I used Delaney Triangulation to triangulate the mean points of Larry David's and Can Ruso's images to find the mean shape.

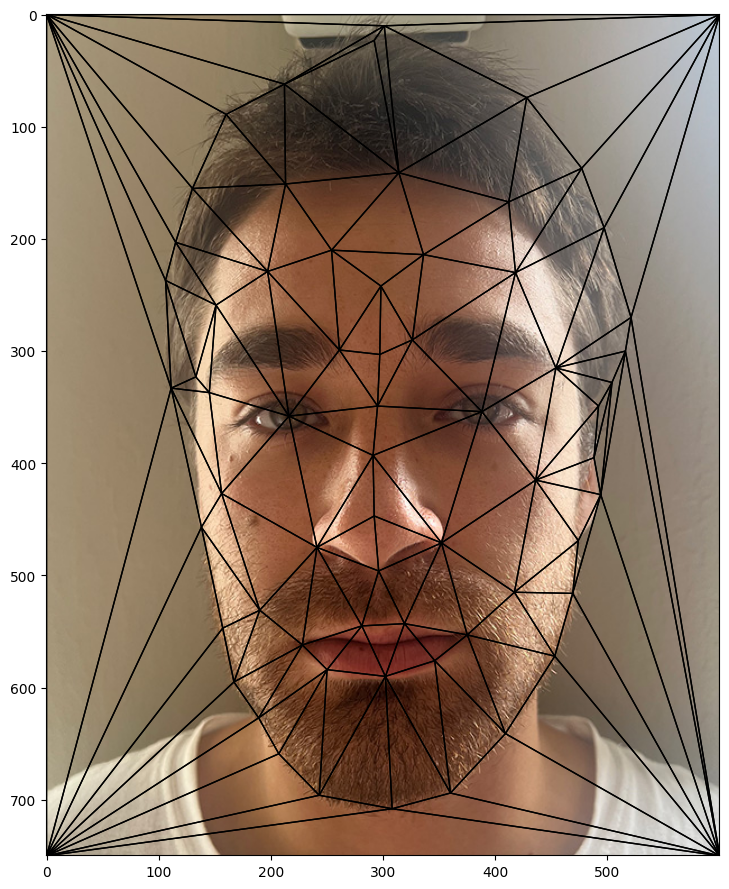
Ruso points

David points

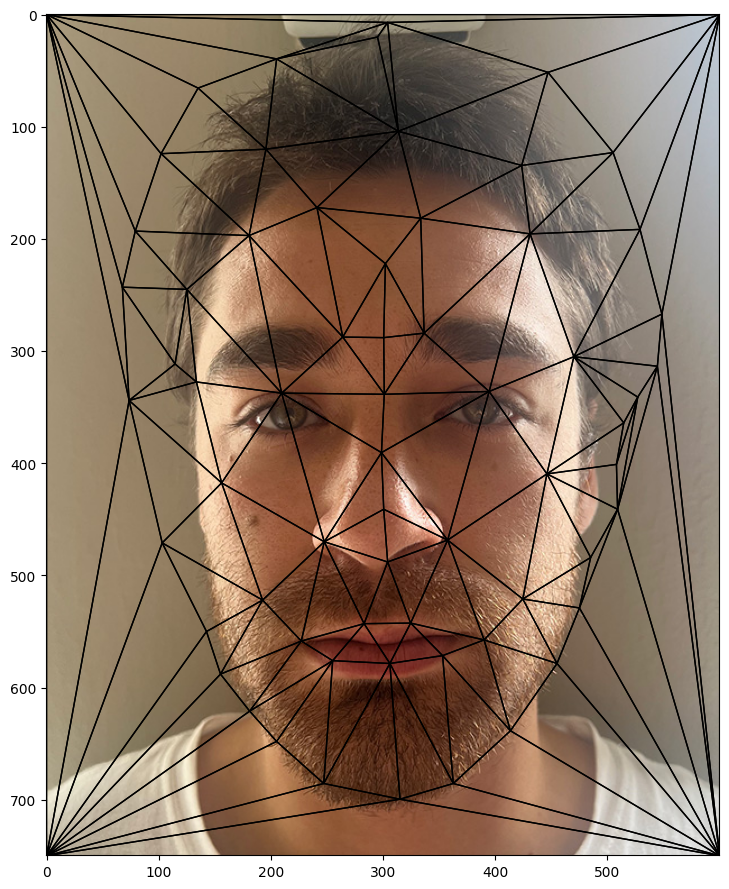
Mean points on Can Ruso

Part 2: Computing the "Mid-way Face"

In order to compute the mid-way face, we need to find the affine transformation matrix that transforms original points from Larry and Can's images to points in each triangle in the average shape triangulation.

Let's say we have two triangles (one is from one of the original shapes, and one is from the average shape):

Original triangle has points p₁, p₂, p₃, with (x_i, y_i) coordinates for each point

Transformed triangle has points q₁, q₂, q₃ with (x'_i, y'_i) coordinates for each point

Then, we can write the following matrix multiplication for the transformation operation, the 1s appended for affine operations:

\[ \begin{bmatrix} a & b & c \\ d & e & f \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_i \\ y_i \\ 1 \end{bmatrix} = \begin{bmatrix} x'_i \\ y'_i \\ 1 \end{bmatrix} \]

If we expand this on all 3 points in the triangles:

\[ \begin{aligned} ax_1 + by_1 + c + 0d + 0e + 0f &= x'_1 \\ 0a + 0b + 0c + dx_1 + ey_1 + f &= y'_1 \\ ax_2 + by_2 + c + 0d + 0e + 0f &= x'_2 \\ 0a + 0b + 0c + dx_2 + ey_2 + f &= y'_2 \\ ax_3 + by_3 + c + 0d + 0e + 0f &= x'_3 \\ 0a + 0b + 0c + dx_3 + ey_3 + f &= y'_3 \end{aligned} \]

We can solve this system in matrix form:

\[ \begin{bmatrix} x_1 & y_1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & x_1 & y_1 & 1 \\ x_2 & y_2 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & x_2 & y_2 & 1 \\ x_3 & y_3 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & x_3 & y_3 & 1 \end{bmatrix} \begin{bmatrix} a \\ b \\ c \\ d \\ e \\ f \end{bmatrix} = \begin{bmatrix} x'_1 \\ y'_1 \\ x'_2 \\ y'_2 \\ x'_3 \\ y'_3 \end{bmatrix} \]

Thus, we can use a linear algebra solver to find a, b, c, d, e, and f, and calculate the transformation matrix.

Once we have the tranformation matrix for every triangle, we use inverse warping to warp original images to the average shape. Since I use inverse warping, the corresponding pixels in the source image can be between pixels so I used RegularGridInterpolator to interpolate the pixel values for dissolving. Applying warping to both of the images, and taking the point-wise average of them gives us the average face. This is basically morphing with warp and morph fraction of 0.5.

Warped Can

Warped Larry

Mid-way Face

Part 3: The Morph Sequence

To produce the morphing sequence, I applied the previous procedure for finding the mid-way face with different warp and dissolve fractions. To create 45 frames, I increase the fractions by 1/45 for each frame. Dissolve fraction determines the weight of source image for the final image while taking the average of the source images. Warp fraction determines how close the shape of final image will be to the source image. Here is a gif with 45 frames for transforming Larry David to Can:

Larry David to Can Ruso

I also applied the morphing sequence to my father and myself. It turns out we look pretty alike:

My father to Me

Part 4: The "Mean face" of a population

For this part, I used all of the data points from Danes dataset to compute the mean face of the population. Firstly, I found the average of all the corresponding points for the given images. I warped all images to the average shape and computed their average to get the mean face. Here are a few examples of the warped images to the average shape:

Here is the mean face of the population:

After computing the mean face of the population, I warped Can's face into the average face, and warped the mean face into Can's face:

Part 5: Caricatures: Extrapolating from the mean

I also caricaturize Can's image. Instead of warping Can's image to the mean shape, we can warp Can's face to can_shape + alpha(can_shape - average_shape) for a negative alpha and a positive alpha > 1 to extrapolate Can's face. These basically exaggerates Can's facial features that are far away from the mean face and the mean face's features that are far away from Can's face. Here are the results:

Part 6: Bells and Whistles

I completed two Bells and Whistles. For the first one, I made a video of myself at different ages. There are 13 different pictures of myself that are morphed sequentially to produce aging effect. I used the morphing sequence defined earlier for each consecutive image. Here is the link:

Link to my video

For the second B&W, I computed the mean face of all the woman images in Danes dataset, and tried to morph only Can's appearance, only Can's shape and both. These are done by having 0 warp frac and 1 dissolve frac, 1 warp frac and 0 dissolve frac, and 0.5 dissolve and warp frac.

Mean Woman Face

Shape only

Appearance only

Both